ENEM - 2016 - INEP

      O censo demográfico é um levantamento estatístico que permite a coleta de várias informações. A tabela apresenta os dados obtidos pelo censo demográfico brasileiro nos anos de 1940 e 2000, referentes à concentração da população total, na capital e no interior, nas cinco grandes regiões.

População residente, na capital e interior segundo as Grandes Regiões 1940/2000

O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é

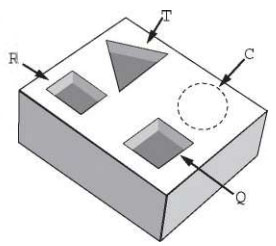
      Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com 10 cm de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfuração de base circular (C).
      O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (I) 3,8 cm; (II) 4,7 cm; (III) 5,6 cm; (IV) 7,2 cm e (V) 9,4 cm.

      Considere 1,4 e 1,7 como aproximações para √2 e √3, respectivamente.

Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?

      Em um exame, foi feito o monitoramento dos níveis de duas substâncias presentes (A e B) na corrente sanguínea de uma pessoa, durante um período de 24 h, conforme o resultado apresentado na figura. Um nutricionista, no intuito de prescrever uma dieta para essa pessoa, analisou os níveis dessas substâncias, determinando que, para uma dieta semanal eficaz, deverá ser estabelecido um parâmetro cujo valor será dado pelo número de vezes em que os níveis de A e de B forem iguais, porém, maiores que o nível mínimo da substância A durante o período de duração da dieta.

      Considere que o padrão apresentado no resultado do exame, no período analisado, se repita para os dias subsequentes.

O valor do parâmetro estabelecido pelo nutricionista, para uma dieta semanal, será igual a

      Um paciente necessita de reidratação endovenosa feita por meio de cinco frascos de soro durante 24 h. Cada frasco tem um volume de 800 mL de soro. Nas primeiras quatro horas, deverá receber 40% do total a ser aplicado. Cada mililitro de soro corresponde a 12 gotas.

O número de gotas por minuto que o paciente deverá receber após as quatro primeiras horas será

      É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada.

Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico?

      Um reservatório é abastecido com água por uma torneira e um ralo faz a drenagem da água desse reservatório. Os gráficos representam vazões Q, em litro por minuto, do volume de água que entra no reservatório pela torneira e do volume que sai pelo ralo, em função do tempo t, em minuto.

Em qual intervalo de tempo, em minuto, o reservatório tem uma vazão constante de enchimento?

      O LIRAa, Levantamento Rápido do Índice de Infestação por Aedes aegypti, consiste num mapeamento da infestação do mosquito Aedes aegypti. O LIRAa é dado pelo percentual do número de imóveis com focos do mosquito, entre os escolhidos de uma região em avaliação.

      O serviço de vigilância sanitária de um município, no mês de outubro do ano corrente, analisou o LIRAa de cinco bairros que apresentaram o maior índice de infestação no ano anterior. Os dados obtidos para cada bairro foram:

      I. 14 imóveis com focos de mosquito em 400 imóveis no bairro;
      II. 6 imóveis com focos de mosquito em 500 imóveis no bairro;
      III. 13 imóveis com focos de mosquito em 520 imóveis no bairro;
      IV. 9 imóveis com focos de mosquito em 360 imóveis no bairro;
      V. 15 imóveis com focos de mosquito em 500 imóveis no bairro.

      O setor de dedetização do município definiu que o direcionamento das ações de controle iniciarão pelo bairro que apresentou o maior índice do LIRAa.

Disponível em: http://bvsms.saude.gov.br. Acesso em: 28 out. 2015.

As ações de controle iniciarão pelo bairro

      A figura representa o globo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfície do globo, passando por B, de forma que o trecho de A até B se dê sobre o paralelo que passa por A e B e, o trecho de B até C se dê sobre o meridiano que passa por B e C. Considere que o plano a é paralelo à linha do equador na figura.

A projeção ortogonal, no plano α, do caminho traçado no globo pode ser representada por

      Diante da hipótese do comprometimento da qualidade da água retirada do volume morto de alguns sistemas hídricos, os técnicos de um laboratório decidiram testar cinco tipos de filtros de água.
      Dentre esses, os quatro com melhor desempenho serão escolhidos para futura comercialização.
      Nos testes, foram medidas as massas de agentes contaminantes, em miligrama, que não são capturados por cada filtro em diferentes períodos, em dia, como segue:

      • Filtro 1 (F1): 18 mg em 6 dias;
      • Filtro 2 (F2): 15 mg em 3 dias;
      • Filtro 3 (F3): 18 mg em 4 dias;
      • Filtro 4 (F4): 6 mg em 3 dias;
      • Filtro 5 (F5): 3 mg em 2 dias.

      Ao final, descarta-se o filtro com a maior razão entre a medida da massa de contaminantes não capturados e o número de dias, o que corresponde ao de pior desempenho.

Disponível em: www.redebrasilatual.com.br. Acesso em: 12 jul. 2015 (adaptado).

O filtro descartado é o

      Em 2011, um terremoto de magnitude 9,0 na escala Richter causou um devastador tsunami no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0 na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala Richter pode ser calculada por

sendo E a energia, em kWh, liberada pelo terremoto e E₀ uma constante real positiva. Considere que E₁ e E₂ representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.

Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).

Qual a relação entre E₁ e E₂?